Materials+ML Workshop Day 7¶

logo

Content for today:¶

  • Supervised Learning Review

    • Regression, Logistic Regression, Classification
    • Train/validation/Test sets
    • Gradient Descent

  • Finish Application: Classifying Perovskites

  • Regression Models

    • Linear Regression
    • High-dimensional Embeddings
    • Kernel Machines (if time)

  • Application: Predicting Material band gaps

The Workshop Online Book:¶

https://cburdine.github.io/materials-ml-workshop/¶

  • A link to our Workshop YouTube playlist is now available

Tentative Week 2 Schedule¶

Session Date Content
Day 6 06/16/2025 (2:00-4:00 PM) Introduction to ML, Supervised Learning
Day 7 06/17/2025 (2:00-4:00 PM) Advanced Regression Models
Day 8 06/18/2025 (2:00-5:00 PM) Unsupervised Learning, Neural Networks
Day 9 06/19/2025 (2:00-4:00 PM) Neural Networks
Day 10 06/20/2025 (2:00-5:00 PM) Neural Networks, + Advanced Applications

Questions¶

  • Intro to ML Content:
    • Statistics Review
    • Linear Algebra Review
  • Supervised Learning
    • Models and validity
    • Training, validation, and test sets
    • Standardizing Data
    • Gradient Descent
    • Classification Problems

Review: Day 6¶

Types of Machine Learning Problems¶

Machine Learning Problems can be divided into three general categories:

  • Supervised Learning: A predictive model is provided with a labeled dataset with the goal of making predictions based on these labeled examples
    • Examples: regression, classification
  • Unsupervised Learning: A model is applied to unlabeled data with the goal of discovering trends, patterns, extracting features, or finding relationships between data.
    • Examples: clustering, dimensionality reduction, anomaly detection
  • Reinforcement Learning: An agent learns to interact with an environment in order to maximize its cumulative rewards.
    • Examples: intelligent control, game-playing, sequential design

Supervised Learning¶

  • Learn a model that makes accurate predictions $\hat{y}$ of $y$ based on a vector of features $\mathbf{x}$.

  • We can think of a model as a function $f : \mathcal{X} \rightarrow \mathcal{Y}$

    • $\mathcal{X}$ is the space of all possible feature vectors $\mathbf{x}$
    • $\mathcal{Y}$ is the space of all labels $y$.

function

Problems with Model Validity¶

  • Even if a model fits the dataset perfectly, we may not know if the fit is valid, because we don't know the $(\mathbf{x},y)$ pairs that lie outside the training dataset:

supervised model ood

Training Validation, and Test Sets:¶

  • Common practice is to set aside 10% of the data as the validation set.
  • In some problems another 10% of the data is set aside as the test set.

supervised split

Validation vs. Test Sets:¶

  • The validation set is used for comparing the accuracy of different models or instances of the same model with different parameters.

  • The test set is used to provide a final, unbiased estimate of the best model selected using the validation set.

Preparing Data:¶

  • To avoid making our model more sensitive to features with high variance, we standardize each feature, so that it lies roughly on the interval $[-2,2]$.
  • Standardization is a transformation $\mathbf{x} \mapsto \mathbf{z}$:
$$z_i = \frac{x_i - \mu_i}{\sigma_i}$$
  • $\mu_i$ and $\sigma_i$ are the mean and standard deviation of the $i$th feature in the training dataset.

Model Loss Functions:¶

  • We can evaluate how well a model $f$ fits a dataset $\{(\mathbf{x}_i, y_i)\}_{i=1}^N$ by taking the average of a loss function evaluated on all $(\mathbf{x}_i, y_i)$ pairs.

Examples:

  • Mean Square Error (MSE):

    $$\mathcal{E}(f) = \frac{1}{N} \sum_{n=1}^N (f(\mathbf{x}_n) - y_n)^2$$

  • Classification Accuracy:

    $$\mathcal{E}(f) = \frac{1}{N} \sum_{n=1}^N \delta(\hat{y} - y) = \left[ \frac{\text{# Correct}}{\text{Total}} \right]$$

Gradient Descent¶

  • Gradient descent makes iterative adjustments to the model weights $\mathbf{w}$:
$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \nabla_w \mathcal{E}(f)$$No description has been provided for this image

Application: Classifying Perovskites¶

  • Finishing up yesterday's application

Today's New Content:¶

Advanced Regression Models

  • Multivariate Linear Regression
    • High-Dimensional Embeddings
  • Regularization
    • Underfitting vs. overfitting
    • Ridge regression
  • Kernel Machines (if time)
  • Application: Predicting Band Gaps of Materials

Multivariate Linear Regression¶

  • Multivariate Linear regression is a type of regression model that estimates a label as a linear combination of features:
$$\hat{y} = f(\mathbf{x}) = w_0 + \sum_{i=1}^D w_i x_i$$
  • If $\mathbf{x}$ has $D$ features, there are $D+1$ weights we must determine to fit $f$ to data.

We can re-write the linear regression model in vector form:

  • Let
$$\underline{\mathbf{x}} = \begin{bmatrix} 1 & x_1 & x_2 & \dots & x_D \end{bmatrix}^T$$

($\mathbf{x}$ padded with a 1)

  • Let $$\mathbf{w} = \begin{bmatrix} w_0 & w_1 & w_2 & \dots & w_D \end{bmatrix}^T$$

(the weight vector)

  • $f(\mathbf{x})$ is just the inner product (i.e. dot product) of these two vectors:
$$\hat{y} = f(\mathbf{x}) = \underline{\mathbf{x}}^T\mathbf{w}$$
  • For these linear regression models, it is helpful to represent a dataset $\{ (\mathbf{x}_n,y_n) \}_{n=1}^N$ as a matrix-vector pair $(\mathbf{X},\mathbf{y})$, given by:
$$\mathbf{X} = \begin{bmatrix} \underline{\mathbf{x}_1}^T \\ \underline{\mathbf{x}_2}^T \\ \vdots \\ \underline{\mathbf{x}_N}^T \end{bmatrix},\qquad\qquad \mathbf{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{bmatrix}$$
  • This is helpful because it allows us to write the MSE (mean square error) model loss function in matrix form:
$$\text{MSE}: \mathcal{E}(f) = \frac{1}{N} \sum_{n=1}^N (\hat{y} - y)^2$$
  • In terms of $\mathbf{X}$ and $\mathbf{y}$, we write:
$$\mathcal{E}(f) = \frac{1}{N}(\mathbf{X}\mathbf{w} -\mathbf{y})^T(\mathbf{X}\mathbf{w} - \mathbf{y})$$
  • It can be shown that the weight vector $\mathbf{w}$ minimizing the MSE $\mathcal{E}(f)$ can be written in closed form:
$$\mathbf{w} = \mathbf{X}^+\mathbf{y}$$
  • $\mathbf{X}^+$ denotes the Moore-Penrose inverse (also called the pseudo-inverse) of $\mathbf{X}$.

Moore-Penrose Pseudo-inverse¶

  • If the dataset size $N$ is sufficiently large such that $\mathbf{X}$ has linearly independent columns, the optimal weights can be computed as:
$$\mathbf{w} = \mathbf{X}^{+}\mathbf{y} = \left( (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\right)\mathbf{y}$$
  • Computing the Pseudo-inverse can be computationally demanding.

High-Dimensional Embeddings¶

  • Often, the trends of $y$ with respect to $\mathbf{x}$ are non-linear, so multivariate linear regression may fail to give good results.

  • One way of handling this is by embedding the data in a higher-dimensional space using many different non-linear functions:

$$\phi_j(\mathbf{x}) : \mathbb{R}^{D} \rightarrow \mathbb{R}\qquad (j = 1, 2, ..., D_{emb})$$

(The $\phi_j$ are nonlinear functions, and $D_{emb}$ is the embedding dimension)

  • After embedding the data in a $D_{emb}$-dimensional space, we can apply linear regression on to the embedded data:
$$\hat{y} = f(\mathbf{x}) = w_0 + \sum_{j=1}^{D_{emb}} w_j \phi_j(\mathbf{x})$$
  • The loss function used in these models is also commonly the mean square error (MSE):
$$\mathcal{E}(f) = \frac{1}{N}(\mathbf{\Phi}(\mathbf{X})\mathbf{w} - \mathbf{y})^T(\mathbf{\Phi}(\mathbf{X})\mathbf{w} - \mathbf{y})$$
  • Above, the quantity $\Phi(\mathbf{X})$ is the embedding of the data matrix $\mathbf{X}$. It is a matrix with the following form:
$$\mathbf{\Phi}(\mathbf{X}) = \begin{bmatrix} 1 & \phi_1(\mathbf{x}_1) & \phi_2(\mathbf{x}_1) & \dots & \phi_{D_{emb}}(\mathbf{x}_1) \\ 1 & \phi_1(\mathbf{x}_2) & \phi_2(\mathbf{x}_2) & \dots & \phi_{D_{emb}}(\mathbf{x}_2) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \phi_1(\mathbf{x}_N) & \phi_2(\mathbf{x}_N) & \dots & \phi_{D_{emb}}(\mathbf{x}_N) \end{bmatrix}$$
  • Fitting a linear regression model in a high-dimensional space can be computationally expensive:
$$\hat{y} = f(\mathbf{x}) = w_0 + \sum_{j=1}^{D_{emb}} w_j \phi_j(\mathbf{x})$$$$\mathbf{w} = \Phi(\mathbf{X})^+\mathbf{y}$$
  • This is especially true if $D_{emb} \gg D$.

Example: Fitting polynomials:¶

  • To fit a polynomial to 1D $(x_i, y_i)$ data, we can use the following embedding matrix:
$$\mathbf{\Phi}(\mathbf{X}) = \begin{bmatrix} 1 & x_1 & x_1^2 & \dots & x_1^{D_{emb}} \\ 1 & x_2 & x_2^2 & \dots & x_2^{D_{emb}} \\ 1 & x_3 & x_3^2 & \dots & x_3^{D_{emb}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_N & x_N^2 & \dots & x_N^{D_{emb}} \end{bmatrix}$$
  • This matrix is referred to as a Vandermonde matrix.

Fitting Complex Models¶

  • High-dimensional embeddings are powerful because they give a model enough degrees of freedom to conform to non-linearities in the data.

  • The more degrees of freedom a model has the more prone it is to "memorizing" the data instead of "learning from it".

  • Fitting a model requires striking a balance between these two extremes.

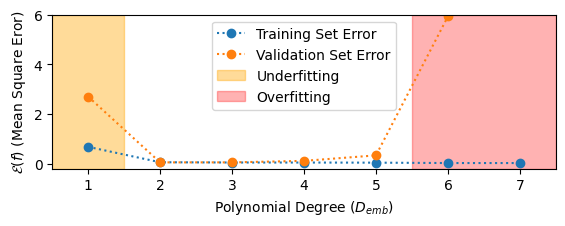
Underfitting and Overfitting¶

  • A model underfits the data if it has insufficient degrees of freedom to model the data.
    • Underfitting often results from poor model choice.
    • When underfitting occurs, both the training and validation error are very high
  • A model overfits the data if it has too many degrees of freedom such that it fails to generalize well outside of the training data.
    • Overfitting results from applying a model that is too complex to a dataset that is too small.
    • When overfitting occurs, the training error plateaus at a minimum (typically at zero) and the validation error increases suddenly.

Example: Polynomial Regression¶

No description has been provided for this image
  • We can diagnose underfitting and overfitting by evaluating the training and validation error as a function of model complexity (in this case, $D_{emb}$).

poly fits

Regularization:¶

  • One way of reducing overfitting is by gathering more data.

    • Having more data makes it harder for a model to "memorize" the entire dataset.

  • Another way to reduce overfitting is to apply regularization

    • Regularization refers to the use of some mechanism that deliberately reduces the flexibility of a model in order to reduce the validation set error

    • A common form of regularization is penalizing the model for having large weights.

  • For most models, a penalty term is added to the overall model loss function.

    • The model minimizes the loss while not incurring too large of a penalty:

    $$\text{ Penalty Term } = \lambda \sum_{j} w_j^2 = \lambda(\mathbf{w}^T\mathbf{w})$$

  • The parameter $\lambda$ is called the regularization parameter

    • as $\lambda$ increases, more regularization is applied.

Ridge Regression¶

  • Ridge Regression is a form of regression directly adds this regularization term to the MSE:
$$\mathcal{E}(f) = \frac{1}{N}(\mathbf{\Phi}(\mathbf{X})\mathbf{w} - \mathbf{y})^T(\mathbf{\Phi}(\mathbf{X})\mathbf{w} - \mathbf{y}) + \underbrace{\lambda(\mathbf{w}^T\mathbf{w})}_{\text{regularization term}}$$
  • For any value of $\lambda$ the optimal weights $\mathbf{w}$ for a ridge regression problem can be computed in closed form:
$$\mathbf{w} = \left((\mathbf{\Phi}(\mathbf{X})^T\mathbf{\Phi}(\mathbf{X}) + \lambda\mathbf{I})^{-1} \mathbf{\Phi}(\mathbf{X})^T \right) \mathbf{y}$$

Exercise: Multivariate Linear Regression¶

  • Computing the Moore-Penrose Inverse
  • Regularized Linear Regression

Kernel Machines¶

  • Kernel machines are an equivalent form of high-dimensional embedding models that avoid computing an embedding entirely:
$$ f(\mathbf{x}) = w_0 + \sum_{i=1}^{D_{emb}} w_i\phi_i(\mathbf{x})\quad \Rightarrow \quad f(\mathbf{x}) = w_0 + \sum_{n=1}^N (\alpha_n - \alpha_n^*)K(\mathbf{x}_n,\mathbf{x})$$

  • Instead of embedding data directly, kernel machines compute only the inner products of pairs of data points in the embedding space.

  • This inner product is computed by a _kernel function $K(\mathbf{x}, \mathbf{x}')$.

  • Kernel machines even allow us to perform linear regression in infinite dimensional spaces!

Application: Band Gap Prediction¶

  • We will work with some data obtained from the Materials Project database to develop a model that predicts the band gap of materials.

Recommended Reading:¶

  • Unsupervised Learning

If possible, try to do the exercises. Bring your questions to our next meeting tomorrow.